
In order to understand this concept, we must first define a force vector.
A force vector is an arrow that represents a force by indicating both magnitude and direction.

The length of the vector represents the magnitude and it points in the direction of the force.
If more than one force vector is drawn on a single sketch, the vectors should be drawn at an appropriate scale so as to indicate relative magnitudes.
That is, if two vectors are drawn and one represents 1000 pounds (vector "A") and the other represents 500 pounds (vector "B") then the vector "A" should be twice as long as vector "B".
Now for the Parallelogram Law:
If we have two force vectors acting on a body and we wish to replace these two vectors with a single vector that has the same effect on the body, we can use the parallelogram law for the addition of force vectors.
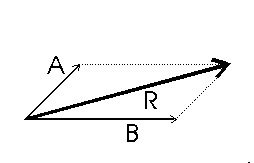
First, draw the two vectors tail to tail.
Next, draw lines parallel to each vector to create a parallelogram.
The resultant force (or the force that can replace the two vectors and still have the same effect of the body as the original two) is the diagonal of the parallelogram (vector "R").
Measure "R" to find its magnitude.
Back to the Engineering Timeline